二叉查找树的解读和实现

Posted on | In |

BST

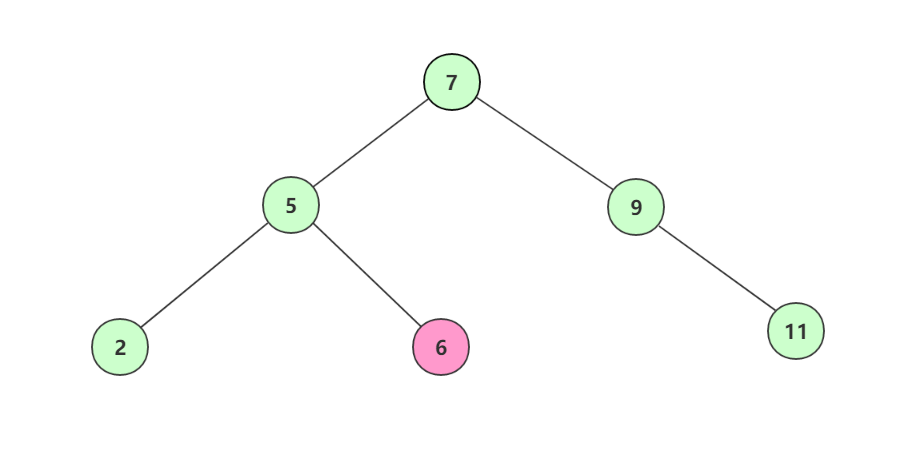
二叉查找树是将一组无序的数据构建成一颗有序数据的树，其设计思想与二分法类似。很好的提高了海量数据查找效率，使得由从头遍历到尾的方式转为二分查找的方式，时间复杂度从O(n)降低为O(log(n))。

概念

  1. 结点：树上的每个元素。
  2. 根结点：没有父结点的结点。
  3. 父结点：结点的上一级结点。
  4. 子结点：结点的下一级结点。
  5. 叶子结点：没有子结点的结点。
  6. 兄弟结点：拥有同一父结点的相邻结点。
  7. 结点的度：一个结点中拥有子结点的个数。
  8. 树的度：树上最大结点的度。
  9. 结点的层次：以根结点为1，每深入一个子结点层次加1。
  10. 树的高度：树中最大的结点的层次。

特性

  1. 左子树所有的结点值均小于，等于根结点值或为空。
  2. 左子树所有的结点值均大于，等于根结点值或为空。
  3. 左、右子树也分别为二叉排序树。
  4. 没有键值相等的结点。

构建

构建二叉查找树，主要把握几条原则，小于当前结点的在左边，大于的在右边，相等的不予处理。但是情况下结合实际业务需求，也可在相等时放在左结点或右结点，但是必须统一规则，不能左右都存在相等的。
创建结点对象：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
package com.ytao.bst;

/**
 * Created by YANGTAO on 2019/11/3 0003.
 */
public class Node {

    private Integer value;

    private Node leftChildren;

    private Node rightChildren;

    public Integer getValue() {
        return value;
    }

    public void setValue(Integer value) {
        this.value = value;
    }

    public Node getLeftChildren() {
        return leftChildren;
    }

    public void setLeftChildren(Node leftChildren) {
        this.leftChildren = leftChildren;
    }

    public Node getRightChildren() {
        return rightChildren;
    }

    public void setRightChildren(Node rightChildren) {
        this.rightChildren = rightChildren;
    }

    public Node(Integer value) {
        this.value = value;
    }
}

创建树的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
package com.ytao.bst;

/**
 * Created by YANGTAO on 2019/11/3 0003.
 */
public class BuildBST {

    private Node rootNode = null;

    public Node build(int[] vals){
        // 遍历所有数据，每次都需从根结点开始寻找左或右子节点为空的位置添加
        for (int val : vals) {
            this.assemble(rootNode, val);
        }

        return rootNode;
    }

    private void assemble(Node node, int val){
        // 创建根结点
        if (node == null){
            rootNode = new Node(val);
        }else{
            // 根据左小右大特性判断
            if (val < node.getValue()){
                Node leftNode = node.getLeftChildren();
                // 如果左子结点为空，就添加为当前结点的左结点，否则继续递归下去
                if (leftNode == null){
                    node.setLeftChildren(new Node(val));
                }else{
                    this.assemble(node.getLeftChildren(), val);
                }
            }else{
                Node rightNode = node.getRightChildren();
                // 如果右子结点为空，就添加为当前结点的右结点，否则继续递归下去
                if (rightNode == null){
                    node.setRightChildren(new Node(val));
                }else{
                    this.assemble(rightNode, val);
                }
            }

        }

    }

}

使用[7,5,9,2,11,6]测试是否满足我们创建树的要求：

1
2
3
4
5
public static void main(String[] args) {
    int[] vals = {7,5,9,2,11,6};
    Node node = new BuildBST().build(vals);
    System.out.println(new Gson().toJson(node));
}

测试结果满足我们要求

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
{
    "value": 7,
    "leftChildren": {
        "value": 5,
        "leftChildren": {
            "value": 2
        },
        "rightChildren": {
            "value": 6
        }
    },
    "rightChildren": {
        "value": 9,
        "rightChildren": {
            "value": 11
        }
    }
}

查找

假设从一百万个数字中获取值为88的数据，如果我们使用遍历的方式，最糟的情况就是排在第一百万个位置的时候，需要我们遍历一百万次才能获取到数据，这就是我们最不想遇到的情况。这时将一百万个数据构建成二叉查找树，我们就可通过树快速找到我们想要的数据。
由于设定一百万个数据比较多，这里我们举例当前拥有数据[7,5,9,2,11,6],我们要找出其中的6。
使用循环遍历所有数据的方法，我们需要6次遍历 7->5->9->2->11->6。
使用二叉查找树查找时，首先构建好的二叉查找树的结构如图：

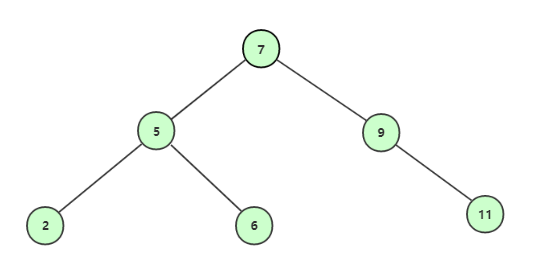
构建二叉查找树
从根结点开始查找；

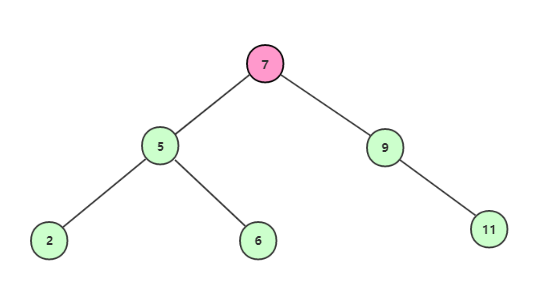
查找根结点
获取根结点7，不等于6，且6<7，所以继续找左子结点；

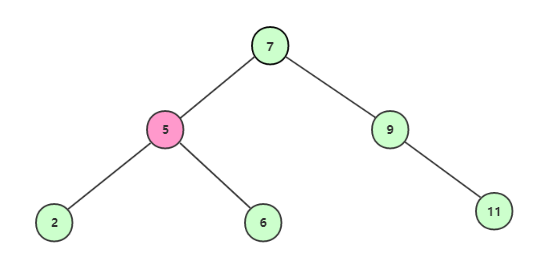
查找子结点
获取到结点5，不等于6，且6>5，所以继续找右子节点；

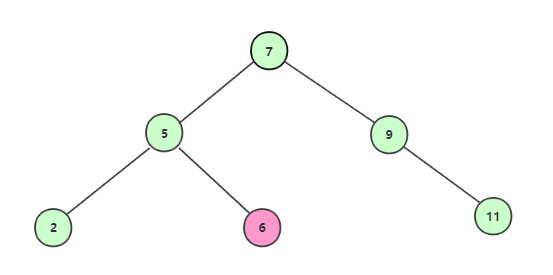
查找子结点
最终获取到结点6，满足我们需要的条件。所遍历的数据为 7->5->6。
代码实现查找：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
package com.ytao.bst;

/**
 * Created by YANGTAO on 2019/11/3 0003.
 */
public class SearchBST {

    public Node search(Node node, int val){
        // 如果结点为空，说明是没有了符合的结点
        if (node == null)
            return null;

        int nodeVal = node.getValue();

        // 如果结点上的键值相等，就是我们需要找的结点
        if (val == nodeVal){
            return node;
        }else if (val < nodeVal){ // 如果小于结点的值，那么一定在结点的左子树中
            return this.search(node.getLeftChildren(), val);
        }else{
            return this.search(node.getRightChildren(), val);
        }

    }


}

插入

二叉查找树的插入规则，必须是要插入后的结点是作为叶子结点。现在向上面的树中插入10，根据上面所分析到的规则，为确保二叉查找树的完整性，最终的插入流程为7->9->11->10：

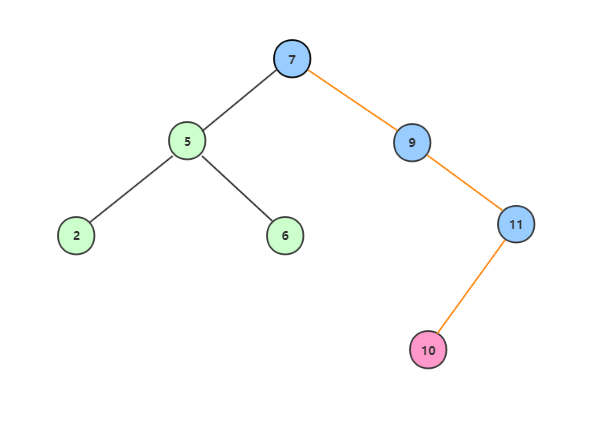
插入10的结点

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
package com.ytao.bst;

/**
 * Created by YANGTAO on 2019/11/3 0003.
 */
public class InsertBST {

    public void inesrt(Node node, int newVal){
        // 当结点为空是，说明是作为根结点
        if (node == null){
            node = new Node(newVal);
        }

        int nodeVal = node.getValue();

        // 如果小于结点的值，插入到左子树中，大于就插入右子树中
        if (newVal < nodeVal){
            Node leftNode = node.getLeftChildren();
            // 为空时，说明为叶子结点，可插入
            if (leftNode == null){
                node.setLeftChildren(new Node(newVal));
            }else {
                this.inesrt(leftNode, newVal);
            }
        }else if (newVal > nodeVal){
            Node  rightNode = node.getRightChildren();
            if (rightNode == null){
                node.setRightChildren(new Node(newVal));
            }else {
                this.inesrt(rightNode, newVal);
            }
        }else {
            // todo 相等时，可根据具体业务处理，放弃，或在左右树中选择一个
        }

    }

}

删除

删除结点分为多种情况，其中主要分析的：

叶子结点

删除叶子结点，将所要删除的叶子结点直接删除便可，比如删除结点6。

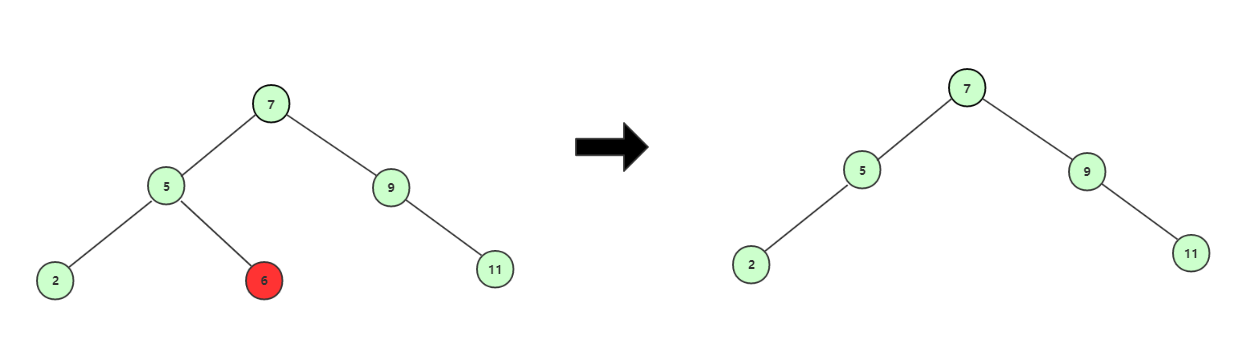
删除叶子结点

单子结点的结点

被删除结点，如果只有一个子结点，那么被删除结点删除后，该结点的子结点补上其位置，比如删除结点9。

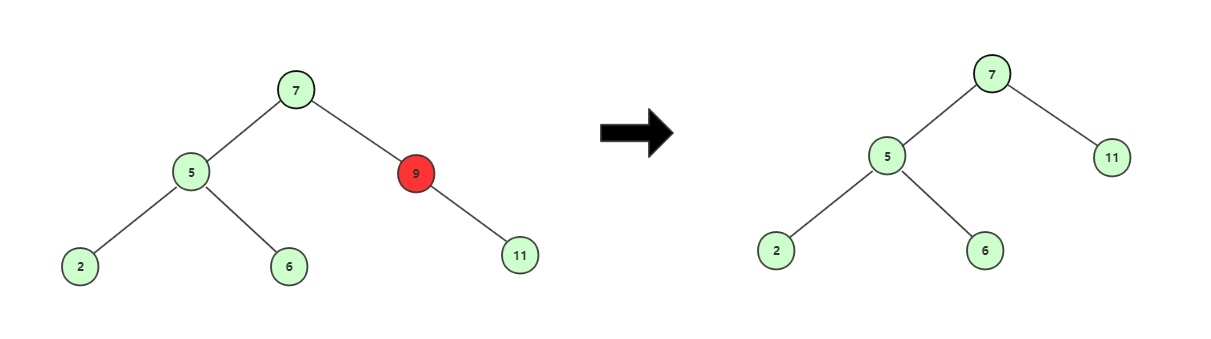
删除单子结点的结点

存在左右子结点的结点

为了更加清楚表达删除存在左右结点的结点，先向树中多添加3个结点8，10，15。然后删除结点9。
这里的解决方法就是，删除9后，可以用前驱结点或后继结点补上。前驱结点为左子树中最大的结点，后继结点为右子树中最小的结点。
现在以后继结点补上的方案为：

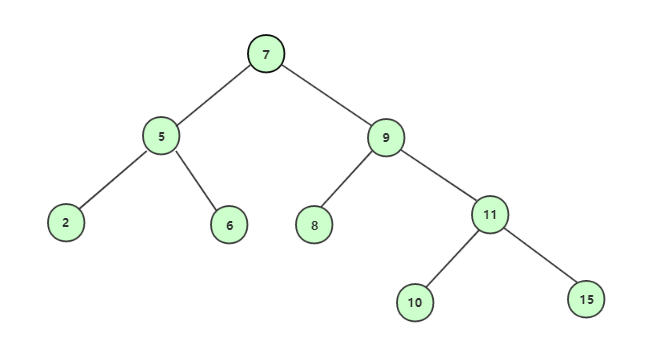
二叉查找树

后继结点补上删除后的结点：

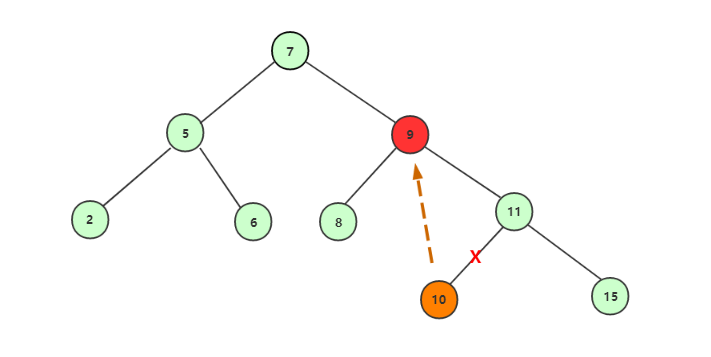
后继结点补上示意图

完成删除，后继结点补充上后：

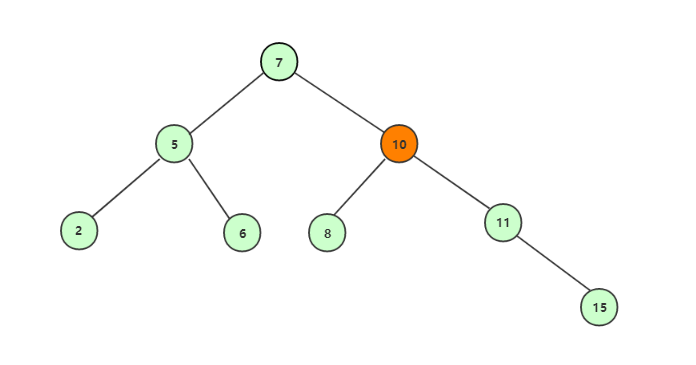
完成删除后的树

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
package com.ytao.bst;

/**
 * Created by YANGTAO on 2019/11/3 0003.
 */
public class DeleteBST {


    public Node delete(Node node, int delVal) {
        // 为空时，代表叶子结点
        if (node == null){
            return node;
        }

        int nodeVal = node.getValue();
        Node leftNode = node.getLeftChildren();
        Node rightNode = node.getRightChildren();

        // 删除的结点，与遍历到的当前结点做比较，小于，大于或等于
        if (delVal < nodeVal){
            Node tempLeftNode = delete(leftNode, delVal);
            node.setLeftChildren(tempLeftNode);
        } else if(delVal > nodeVal){
            Node tempRightNode = delete(rightNode, delVal);
            node.setRightChildren(tempRightNode);
        } else {
            // 删除的结点与当前遍历到的结点相等时
            // 并且左结点为空时，返回右结点去补上删除的位置，反则返回左结点补上
            // 说明删除结点为单子结点的情况
            if (leftNode == null){
                return rightNode;
            } else if (rightNode == null){
                return leftNode;
            }

            // 通过查询最小右结点，获取后继结点
            Node minNode = minNode(rightNode);
            int minNodeValue = minNode.getValue();
            node.setValue(minNodeValue);
            // 删除后继结点
            Node tempRightNode = delete(rightNode, minNodeValue);
            node.setRightChildren(tempRightNode);
        }
        return node;
    }

    private Node minNode(Node node) {
        // 一直寻找最小值，知道左子节点为空为止
        Node leftNode = node.getLeftChildren();
        if (leftNode != null)
            return minNode(leftNode);
        return node;
    }

}

至此上面三中情况都予满足。

总结

上面对二叉查找树的操作都已介绍，但是正真使用中，是要结合实际业务进行相关调整来满足自己的需求，不然，一切的优化手段都是假把式。二叉查找树虽然好用，但是它也是有一定要求，在数据量不大的情况下，使用遍历的方式，更加符合我们的要求，所以它使用场景一般是在海量数据的查询，用来提查询效率。

wechat
我的公众号
原创技术分享，感谢您的鼓励！
0%